이득우의 게임수학_입문_5. 회전의 수학 I : 삼각함수

5. 회전의 수학 I : 삼각함수
강의 링크 : https://youtu.be/tuqarT4mUZg?feature=shared

이번 강의에서는 회전에 대한 수학을 이야기할 예정입니다.

회전이란 무엇일까요?

앞 강의에서 트랜스폼은 결국 크기, 회전, 이동이라는 세가지변환을
순서대로 변환해주는 합성 변환이라고 하였습니다.

이 중에서 ‘회전’은 별도로 주제를 떼서 설명할 만큼 독특한 변환입니다.
우리가 현실세계에서 회전을 한다면
중심축을 설정하고 물체를 돌리면 되겠죠.

하지만 게임에서의 변환은 가상세계에서 공간이 돌아간다는 개념이었습니다.
따라서 가상 세계에서 회전을 구현하기 위해서는
물체가 돌아가는 것이 아니라 공간이 돌아가야 합니다.
❓ 그렇다면 이 무한대로 뻗어있는 벡터 공간을 어떻게 돌려야 할까요?

지난 강의에서 표준 기저 벡터에 대해 설명했습니다.
어떤 벡터 공간을 집이라고 한다면
이를 떠받을고 있는 주춧돌로 표준 기저 벡터를 설명할 수 있습니다.

벡터 공간의 모든 벡터는
표준 기저 벡터에 선형 조합으로 만들어지기 때문입니다.
❓ 그렇다면 이 표준 기저 벡터를 변경하면 어떻게 될까요?

벡터 공간에 속한 모든 원소들이
표준 기저벡터가 변화된 모습에 따라서 모두 다시 재배치가 될 것입니다.
이것이 바로 공간 변환의 원리라고 할 수 있습니다.
이 원리를 바탕으로 회전을 어떻게 구현하는지 알아보겠습니다.
▶️ 회전 변환의 원리

회전 변환이 가지고 있는 특징 중의 하나는 물체의 모습이 변하지 않습니다.
따라서 두 표준 기저 벡터가 어떻게 변했을 때
이 두 표준 기저 벡터가 가지고 있었던 성질을 그대로 똑같이 유지해주면
회전 변환이 될 수 있습니다.
그렇다면 2차원 평면을 구성하는 구성하는
두 표준 기저 벡터는 어떤 성질을 가지고 있는지 한번 살펴보겠습니다.

그림에서 보는 것처럼 먼저 각 표준 기저 벡터는 항상 1 입니다.
그리고 두 표준 기저벡터는 서로 직교하고 있습니다.
이렇게 두 표준 기저벡터와 가지고있는 크기가 1,
서로 직교하는 성질을 우리가 계속 유지 시켜주면 회전 변환을 만들 수 있습니다.
❓ 2차원 평면에서 크기가 1인 벡터를 나열하면 어떻게 될까요?

위 그림처럼 동그란 원이 만들어집니다.
✔️ 이렇게 반지름이 1인 원을 단위원이라고 합니다.
단위원 상에 위치한 두 벡터를 임의로 뽑는다면
첫번째 조건인 크기가 1인 2개의 벡터를 가져올 수가 있게 됩니다.

이런 두 개의 벡터 중에서 서로 직각을 이루는 어떤 쌍을 발견해서 가져온다면
이것은 표준 기저 벡터가 가지고 있는 성질을 그대로 유지하는
두 개의 새로운 벡터라고 할 수 있습니다.
이것이 바로 2차원 공간에 회전 변환의 원리 입니다.

3차원, 4차원 회전도 마찬가지 입니다.
그렇다면 원 위의 점을 어떻게 가져올 수가 있을까요
이를 가져오기 위해선 삼각 함수에 대해서 이해를 해야 합니다.

원 호 위의 한점을 표현할 때
직교 좌표계 상에서 ( x, y ) 라는 데이터를 사용해서 표현할 수가 있지만
회전이라는 행동에 관점에선 기준 위치에서 얼만큼의 각을 사용해서 회전 했는지,
회전한 각과 반지름을 사용해서 표현할 수가 있습니다.

이 그림에서 수선을 내리면 직각삼각형이 만들어집니다.

이 직각 삼각형은 빗변, 밑변, 높이 3가지 구분으로 구성이 되어 있습니다.
✔️ 이것을 조합해서 만든 비를 삼각비라고 합니다.

대표적인 삼각비로는 위 3가지 종류가 있습니다.

✔️ 여기서 파생된 것이 삼각함수 입니다.
삼각형이란 도형은 모든각이 90도 이내여야 한다는 그런 제약이 있지만,
이러한 비율을 원으로 확장해서 함수로 표현한 것이 바로 삼각함수 입니다.

위 공식을 삼각함수에서는 sin, cos, tan 함수로 이야기 합니다.
그렇다면 원 상에 위치한 하나의 벡터를 삼각함수를 사용해서 가져올 수가 있습니다.
❓ 어떻게 가져올 수가 있을까요?

위 그림을 보면 위 단위원의 반지름의 크기가 1이면

빗변 분의 밑변은 밑변이 되고,
빗변 분의 높이는 높이가 됩니다.

원 상에 위치한 임의의 한 점 삼각함수로 표현 한다면
( cos θ , sin θ ) 입니다.

x축에 해당하는 것은 밑변인데 이것은 cos 함수와 관련이 있고
y축에 해당하는 것은 높이인데 이것은 sin 함수와 관련이 있습니다.
두 값을 늘려가면 파형을 만드는 것을 확인할 수 있습니다.

여기에서 우리가 필요로 하는것은
직교하는 두개의 표준 기저 벡터가 임의의 각 θ 라는게 주어 졌을 때
어떻게 변화 되는지 그 좌표를
삼각함수를 사용해서 얻어 낸다는 겁니다.
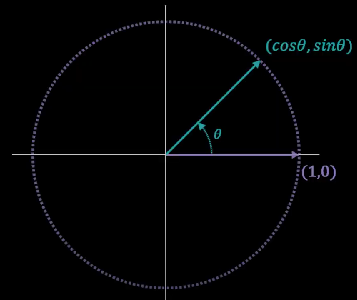
먼저 첫번째 표준기저 벡터 (1,0) 에 대해 살펴보겠습니다.
이것은 바로 cos θ 와 sin θ 좌표로 변환이 됩니다.

그렇다면 첫번째와 직교하는 두 번째 표준 기저 벡터가
각 θ 만큼 회전한 것은 어떻게 될까요?

두 삼각형은 합동이기 때문에 두 번째 표준 기저 벡터가 회전한 좌표는
( -sinθ , cosθ )가 됩니다.

따라서 회전된 평면 공간이란 결국 두 표준 기저 벡터 ( 1, 0 )과 ( 0, 1 )를
두 벡터 ( cosθ , sinθ )와 ( -sinθ , cosθ )로 재구성한 공간이라고 말할 수 있습니다.

어떤 점 벡터 공간의 임의의 점 ( x, y )를 각 θ 만큼 회전을 시켰다고 하면
위처럼 계산할 수가 있습니다.
결과가 조금 복잡합니다. 수학자들은 이러한 변환을 쉽게 계산하기 위해서
새로운 방법을 고안 했는데,

그것이 바로 이전 강의에서 언급한 행렬입니다.
그렇다면 이러한 행렬을 어떻게 해서 해결해야 할까요?

지금 이 행렬을 살펴보면, 앞서서 첫번째 표준 기저 벡터와
두번째 표준 기저 벡터와 각각 변환값을 구했었는데,

그것들을 하나씩 열로 꽂아준 결과라고 볼 수 있습니다.
이것이 바로 행렬의 설계 원리 입니다.
이렇게 2차원 평면에서 진행하는 회전변환에 알아봤습니다.
우리가 실제로 사용할 3차원 공간에서의 회전은 보다 까다롭습니다.
3차원 공간에서 임의의 2차원 평면을 설정하고 그것에 따라 돌려줘야 하기 때문입니다.

게임에서는 이를 위해서 크게 두가지 방식을 사용합니다.
3차원 공간에서 임의의 회전축을 하나 설정합니다.
돌릴 점이 속해있는 평면을 하나 만들고 그 평면을 따라서 회전을 시켜주는 방법이 있습니다.
✔️ 이것을 축-각 회전이라고 합니다.

다른 방법으로는 x, y, z 세개의 표준 기저 벡터를 중심축으로 잡고
지정된 순서에 따라서 하나씩 하나씩 돌려서 총 3번 돌려주는 방식을 사용하기도 합니다.
✔️ 이것을 오일러 각 회전 이라고 합니다.
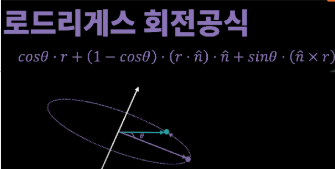
첫번째 축-각 방식의 대표적 방법으로는 로드리게스 회전공식이 있습니다.
공식이 조금 복잡한데, 내적 연산과 외적 연산 문제로 잘 활용하고 있습니다…

오일러 각 방식은 하나의 회전을 일부러 세 번의 회전으로 나누어 쪼개서 진행하는 방식입니다.
기본 회전축은 우리가 다 인지하고 있는 표준 기저 벡터를 사용하고 있기 때문에
회전축에 대한 정보는 생략하고, 그냥 얼만큼 돌아갔는지 각에 대한 정보만 저장하는 방식입니다.

이 방식은 직관적이고, 데이터가 적게 사용되기 때문에
대부분 3차원 소프트웨어에서 물체의 회전을 지정할 때 많이 사용합니다.
❗그런데 이 두가지 방식 모두 단점이 있습니다.

로드리게스 회전은 행렬로 만들기가 까다롭습니다.
행렬로 변환하지 않으면, 전체 렌더링을 구성하는 렌더링 파이프라인의 흐름이 끊기게 됩니다.
그래서 역으로 효율이 떨어지는 문제가 발생할 수가 있습니다.

오일러 각 방식은 손쉽게 행렬로 만들 수 있는 반면에
한번에 회전을 3번으로 끊어서 표현하기에
임의의 축에 대해서 부드럽게 회전하는 움직임을 표현할 때
매 움직임마다 세 번씩 끊어서 다시 재계산해야 하기 때문에
비효율적이고 까다롭다는 문제가 있습니다.

그리고 가끔가다가 한 축의 회전이 증발되어 버리는 짐벌락이라는 현상도 발생합니다.

그렇다면 3차원 회전을 안정적으로 구현할 수가 있을까요?

수학자들과 공학자들은 이런 문제를 해결하기 위해서
다차원의 수체계를 사용해서 해결했습니다.
그것이 바로 사원수 (Quaternion) 입니다.
다음 영상에서는 이 사원수에 대해 알아보겠습니다.